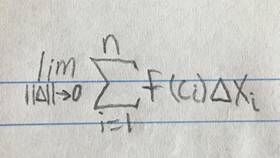Определенный интеграл функции на отрезке можно представить как предел интегральных сумм. Это фундаментальное понятие математического анализа связывает интегральное и дифференциальное исчисление.
Содержание
Определение интеграла через предел суммы
| Элемент | Описание |
| Разбиение отрезка | a = x₀ < x₁ < ... < xₙ = b |
| Диаметр разбиения | max Δxᵢ = max(xᵢ - xᵢ₋₁) |
| Интегральная сумма | Σ f(ξᵢ)Δxᵢ, где ξᵢ ∈ [xᵢ₋₁, xᵢ] |
Формальное определение интеграла Римана
Функция f интегрируема по Риману на [a,b], если существует предел интегральных сумм при стремлении диаметра разбиения к нулю:
∫ab f(x) dx = limλ→0 Σi=1n f(ξᵢ)Δxᵢ
Геометрическая интерпретация
Для положительных функций
- Интегральная сумма - сумма площадей прямоугольников
- Предел суммы - площадь под кривой
- Δxᵢ → 0 увеличивает точность приближения
Типы интегральных сумм
| Тип суммы | Выбор точки ξᵢ |
| Нижняя сумма Дарбу | inf f(x) на [xᵢ₋₁, xᵢ] |
| Верхняя сумма Дарбу | sup f(x) на [xᵢ₋₁, xᵢ] |
| Сумма Римана | Произвольная точка в отрезке |
Критерий интегрируемости
Функция f интегрируема по Риману тогда и только тогда, когда:
- Она ограничена на [a,b]
- Для любого ε > 0 существует разбиение, где верхняя и нижняя суммы Дарбу отличаются менее чем на ε
Пример вычисления предела суммы
Интеграл от x² на [0,1]
- Равномерное разбиение: xᵢ = i/n
- Выбор ξᵢ = xᵢ
- Интегральная сумма: Σ (i/n)² · (1/n)
- Предел суммы: lim (n(n+1)(2n+1))/(6n³) = 1/3
Связь с первообразной
Согласно основной теореме анализа, если F - первообразная f, то:
∫ab f(x) dx = F(b) - F(a)
Это устанавливает связь между пределом сумм и антидифференцированием.
Обобщения понятия интеграла
- Интеграл Лебега - более общий подход
- Кратные интегралы - для функций многих переменных
- Криволинейные интегралы - по кривым и поверхностям